画像をダウンロード 弧長 扇形 面積 公式 151397

はじめに 半径が「r」、中心角が「θ」である扇の面積「S」は で求めることができました。 ここでは、 中心角「θ」が与えられていない その代わりに弧の長さ「l」は与えられている 場合に扇の面積を求める公式を紹介しましょう。 半径「rθ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos ⁡ θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l 関連リンク 楕円の弧長の求め方 お客様の声 アンケート投稿 よくある質問教科書には扇形の面積や弧の長さを求める公式があります。 半径を\(\,r\,\)，中心角 \(\,a^\circ\,\) として、 扇形の弧の長さ \(\,\ell\,\) と扇形の面積 \(\,S\,\) の公式は、

扇形計算公式 一條弧和經過這條弧兩端的兩條半徑所圍成的圖形叫扇形 半 華人百科

弧長 扇形 面積 公式

弧長 扇形 面積 公式-為求得此弧邊面積，先以正五邊形作為試驗 ── 分割中央弧邊面積 先將中央弧邊面積以OB OC中心分割成五分之一，並連──接 AB AC 。且 OBC面積 = 扇形ABC面積 – 2 ΔOAB面積。 ──About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

扇形的弧長與面積公式： 若圓半徑為 r ，扇形 COD 的圓心角 ∠ COD ＝θ（弧度），0 ≤ θ ≤ 2π， 如下圖所示，令扇形的弧長為 s ，面積為 A ，則：扇形的弧長與面積 扇形的弧長與面積 1弧長扇形的弧長我們要怎麼求得呢 2扇形面積 這樣以後題目給我們半徑r，跟角度要我們求扇形的弧長或面積，我們就可以輕鬆的套公式把它算出來了 弧 の 長 さ 半 径 中 心 角 弧 の 長 さ = 半 径 × 2 × 314 × 中 心 角 360 ∘ 中心角のわかっている、おうぎ型の 面積 を求める公式 面 積 半 径 半 径 中 心 角 面 積 = 半 径 × 半 径 × 314 × 中 心 角 360 ∘ 面積を2倍 にすると 面 積 半 径 半 径 中 心 角 面 積 ×

 扇形の面積の公式弧度法 半径が r 、中心角が \theta (\mathrm {rad}) の扇形の面積 S は \begin {align} \color {red} {S = r^2 \pi \cdot \frac {\theta} {2\pi} = \frac {1} {2} r^2 \theta} \end {align} 弧度法では 360^\circ が 2\pi \ \mathrm {rad} に対応するので、中心角の割合は「 \displaystyle \frac {\theta} {2\pi} 」となります。 扇形の公式はこう変わる 弧度法の定義は扇形の弧の長さ を半径 で割ると, 角 が求まるというもので, 以下の式で定義されます。 この定義から, 扇形の弧の長さ は, と導け, 扇形の面積 は, 度数法の公式 をradに置き換えて, また, 扇形の弧の長さの公式よりHyperbolic Arch(1) areay=ba√x2−a2S=abcosh−1xa(2) eccentricitye=√a2b2a(3) hyperbolic archk=1e,z=√x2−a2x2−(ka)2L=1k{a(1−k2)F(z,k)−aE(z,k)xz}Hyperbolic Arch(1) areay=bax2−a2S=abcosh−1⁡xa(2) eccentricitye=a2b2a(3) hyperbolic archk=1e,z=x2−a2x2−(ka)2L=1k{a(1−k2)F(z,k)−aE(z,k)xz} お客様の声 アンケート投稿

 "扇形の弧の長さと面積"の公式とその証明です！ 扇形の弧の長さと面積公式扇形の弧の長さと面積半径r、中心角θ、弧の長さl、面積Sとすると \(・l＝rθ\) \(・S=\frac{1}{2}r^2θ=\frac{1}{2}lr\)証明扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角（単位「度」）を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題の解き方 を説明しています弧度法で扇の弧の長さと面積を求める公式 弧度法を使って、扇の弧の長さと面積を求める公式を紹介します。 半径がr、中心角がθの扇の弧の長さをl、面積をSとするとき ※θは、度数法ではなく弧度法

扇形的面积公式 弧长公式 环球信息网

Q Tbn And9gcqvlkvltyrw1 Uqrhidvg8g3sxdrak8626y9ldlzswaeck4kxwm Usqp Cau

扇形の弧の長さlも、同様の関係を利用し l=rθ の式が誘導できます。よって、扇形の面積は下式で表すことも可能です。 s＝r 2 θ／2＝lr／2 扇形の弧の長さは、詳細は下記が参考になります。 扇形の弧の長 2分でわかる！扇形の弧の長さを求める公式 「扇形の弧の長さ」の求め方の基本はわかったね？？ それじゃあ、 扇形の弧の長さの公式 をみていこう！ 扇形の半径をr、中心角をα、円周率をπとすると、 2πr×α/360 で「扇形の弧の長さ」を求められるんだ。弧の長さと面積の公式 ＜証明＞ 弧の長さと面積の公式の証明をしておきます。 証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。

六年级扇形面积和弧长公式 初三网

扇形平台钢格板怎么计算弧长和扇形面积 安平润潭金属网业www Runtanwangye Com

式 扇形 A = 面積 L ＝ 円周の長さ R ＝ 半径 扇形 A = 面積 L ＝ 弧の長さ α ＝ 角度 (DEG) α ＝ 角度 (rad) A = 面積 L ＝ 弧の長さ α ＝ 角度 (DEG) α ＝ 角度 (rad) 弓形即， \(扇形面積 = \pi r^{2} \times \dfrac{\theta}{360^{\circ}} \) 同一個定理，按圓形周界同弧長嘅比例 \(弧長 = 2\pi r \times \dfrac{\theta}{360^{\circ}} \)7月 17, 15 謝語蘭 男女話題 關於弧長圓面積扇形面積 (簡單唄) Yahoo!奇摩知識 圖片來源 via 圖片來源 via 圖片來源 via 圖片來源 via via扇形面積公式 1/2 (r)^2Θ 弧長公式 r Θ (Θ為角度) 參考資料： 我自已 1 001 意見者： MrNatural ( 初學者 2 級 ) 發表時間： 0145 檢舉 ~老人家

初三中考正多边形和圆弧长和扇形面积专项复习下载 Word模板 爱问共享资料

弧长和扇形面积公式 搜狗图片搜索

數學領域數學 學習階段： 國小56年級 (三) 學習內容： S63 圓周率、圓周長、圓面積、扇形面積：用分割說明圓面積公式。 求扇形弧長與面積。 知道以下三個比相等：（1）圓心角：360；（2）扇形弧長：圓周長；（3）扇形面積：圓面積，但應用問題只處理用（1）求弧長或面積。 學習表現： sⅢ2 認識圓周率的意義，理解圓面積、圓周長、扇形面積與弧長之計算方式。Scipursuit 算数・数学 扇形の弧の長さの求め方 公式と計算例 扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角（単位「度」）を表します。 このページの続きでは、この 公式の導き方 と、 扇形の弧の長さを求める計算問題の解き方 を説明 Part 2 Part 2弧度法(ラジアン)今までの角度(0°,180°,360°等)＝度数法(「°」 図解講師「爽茶」の最高に分かりやすいサイト そうちゃ's 図解英数ゼミナール弧度法で弧の長さと面積をだす公式が腑に落ちません弧の長さは、半径 x 中心角(ラジアン)面積は、半径 x この長さ x 1／2とのことですが、なぜ上記の公式で、弧の長さと、面積を求めることができるのでしょうか？

弧长公式 扇形面积公式 圆 中考网

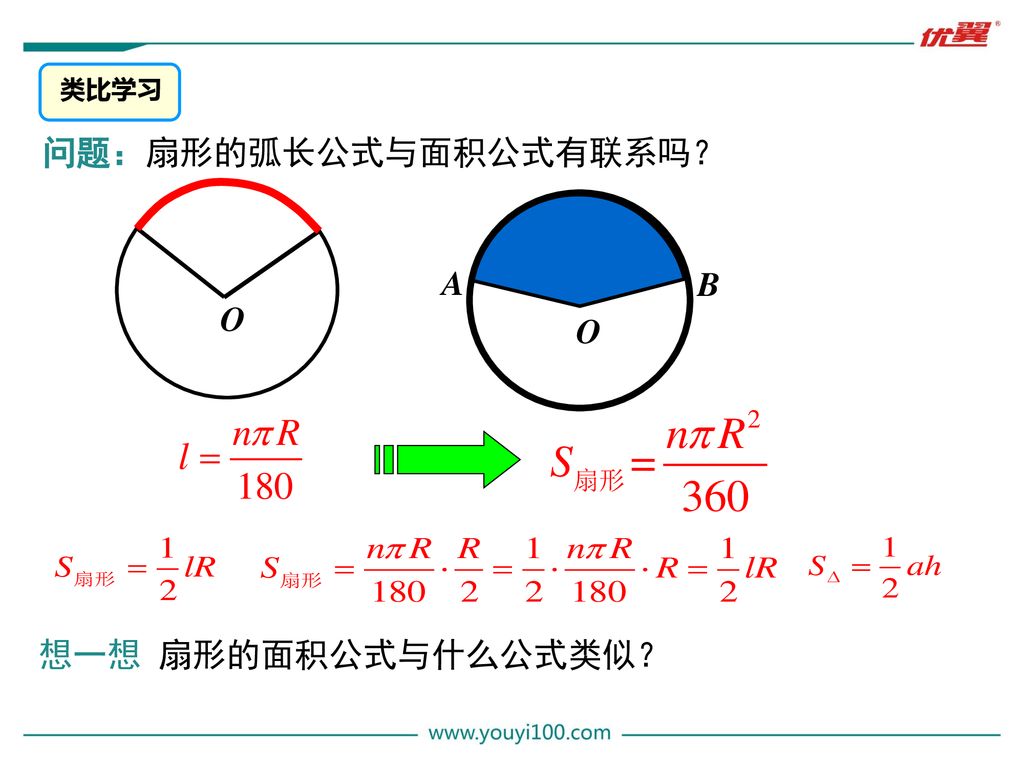
第二十四章圆24 4 弧长和扇形面积第1课时弧长和扇形面积学练优九年级数学上 Rj 教学课件优翼课件导入新课讲授新课

放物線面積、弧長の公式はすぐに忘れてしまうので便利 ご意見・ご感想 放物線は基本的にすべて相似形でありこの場合、三点（b/2,0) (0,a) (b/2,0)をとおる、y＝Mx*2aの形の放物線であり、半徑云々は無関係に計算できますね。 5 1555 男 / 60歳以上 / その他 / 役に立った / 使用目的 ソーラークッカー反射面長の計算、速くてよい。 6 22 男 / 30歳代弧度法における弧の長さの公式 半径 r r r ，中心角 θ \theta θ ラジアンの扇型の弧の長さは r θ r\theta r θ 例えば，半径が 2 2 2 で中心角が π 4 \dfrac{\pi}{4} 4 π ラジアンである扇形の弧の長さは， 2 × π 4 = π 2 2\times\dfrac{\pi}{4}=\dfrac{\pi}{2} 2 × 4 π = 2 π と計算でき 扇形のまわりの長さは、 扇形の弧の長さ＋半径×2 で求められます。 この扇形の弧の長さ＝18×314× 1 ° 360 ° ＝14（cm） よって、求める扇形のまわりの長さは 14＋9×2＝3684（cm） 答え 3684㎝ ～平面図形の面積・まわりの長さを求める公式まとめ

弧长及扇形的面积公式 弧长及扇形面积计算公式

高中數學 三角函數 數乙 弧長與扇形面積公式ii 曾政清 Youtube

扇形の弧の長さと面積を出すためには、その前に円周と面積を必ず出さなければいけません。 そのため、小学校の算数のおさらいをしましょう。 円周や面積については、以下の公式によって計算します。 円周 ＝ 直径 × 314（円周率） 円の面積 ＝ 半径 × 半径 × 314（円周率） ただ中学数学では、円周率として314を使いません。 314は正確な数値ではなく近似値普高數學 / 高三數學 / 數學甲上 / 二、三角函數 / 三角函數的性質與圖形 / 11弧度、弧長與扇形面積 DeltaMOOCx 47K subscribers Subscribe 高中 數學 吳汀菱 三角函數 三角函數的性質與圖形 弧度、弧長與扇形面積 1080 0707 Watch later Share円弧の長さ (L) =B1*RADIANS (B2) 3 弦の長さ (c) =2*B1*SIN ( RADIANS (B2/2)) 2 面積 (S) =B1^2*RADIANS (B2)/2

高一 高一期末复习专题 6 弧长公式 扇形面积公式

扇形計算公式 一條弧和經過這條弧兩端的兩條半徑所圍成的圖形叫扇形 半 華人百科

この証明における不備は、扇形OAP の面積がθ 2 となるところにある。 もう少し詳しく説明すると、扇形の面積の公式 扇形の面積= (弧長£ 半径)¥2 を導く際に、lim θ!0 sinθ θ = 1 という事実を用いているところにある。証明しよ上式の通り、扇形の面積は、扇形の弧の長さlに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は？1分でわかる意味、公式、求め方、ラジアンとの関係 扇形の弧の長さとラジアンの関係 扇形の弧の長さを求める公式は lC 扇形弧長S=rθ d 扇形面積A=1 2 r2θ=1 2 rS (2)三角函數的定義 正弦函數sinA=∠ 的對邊 斜邊 餘弦函數cosA=∠ 的鄰邊 斜邊 正切函數tanA=∠ 的對邊 ∠ 的鄰邊 餘切函數cotA=∠ 的鄰邊 ∠ 的對邊 正割函數secA= 斜邊 ∠ 的鄰邊 餘割函數cscA= 斜邊 ∠ 的對邊 (3)三角函數的關係

扇形弧长公式计算方法 北京爱智康

弧长和扇形面积 圆ppt 第一课时 第一ppt

 扇形の面積 ＝ 弧の長さ × 半径 ÷ 2 なんとなく、三角形の面積と同じように面積を求めることができてしまうのです。 では、どうしてこのようなことがいえるかを考えて見ましょう。 扇形の面積を求める公式は前に述べたとおり以下の公式です。 扇形の 「扇形の面積の公式」を忘れたら「ピザ」を思い出そう笑 まとめ：扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった？？ 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360おうぎ形の公式 弧の長さ ＝ 円周 × 中心角 360° 中 心 角 360 ° ＝ 直径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積 ＝ 円の面積 × 中心角 360° 中 心 角 360 ° ＝ 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時に

Ppt 弧长和扇形面积powerpoint Presentation Free Download Id

1

 扇形の公式にあてはめると S = 3×3×π×90/360 = 9π/4S = 1 2 r 2 (θ − sinθ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos ⁡ θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l ( 3) e l l i p t i c a l c o r d c = r ( θ 0) 2 r ( θ 1) 2 − 2 r ( θ 0) r ( θ 1) cos ⁡ ( θ 1 − θ 0)

九年级数学上册教案24 4 弧长和扇形面积第1课时弧长和扇形面积下载 Word模板 爱问共享资料

扇形面积计算公式

馬雲：看懂了，等於讀了 3 年 mba！ 你不成熟的4大特徵

弧长及扇形的面积公式 弧长及扇形面积计算公式

弧长及扇形的面积公式 弧长及扇形面积计算公式

圓與扇形的周長與面積計算 每日頭條

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

例題 如何計算扇形的弧長 六年級 圓周長與扇形周長 均一教育平台

九年级数学 圆 弧长和扇形面积 每日头条

弧长及扇形的面积公式 弧长及扇形面积计算公式

24 4弧长和扇形面积圆锥的侧面积和全面积 Ppt Download

弧長計算公式 弧長公式 N是圓心角度數 R是半徑 L是圓心角弧長 L 華人百科

扇形面積公式弧長14 Zilhc

扇形面积的计算公式 扇形的面积计算公式

扇形面积和弧长公式 搜狗图片搜索

2 圓心角所對弦長 弧長與扇形面積 基本觀念 國三上2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube

扇形面积的计算公式 扇形的面积计算公式

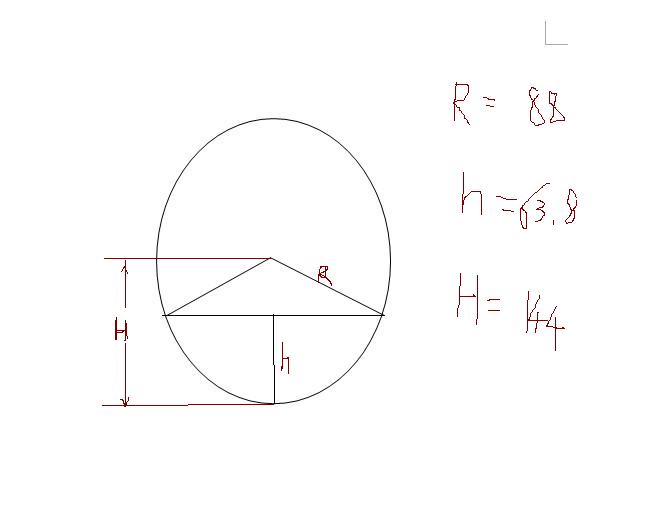
扇形面積 面積公式 另解 公式推導過程 中文百科全書

高一 高一期末复习专题 6 弧长公式 扇形面积公式

3 6 弧长和扇形面积的计算 Page105 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网

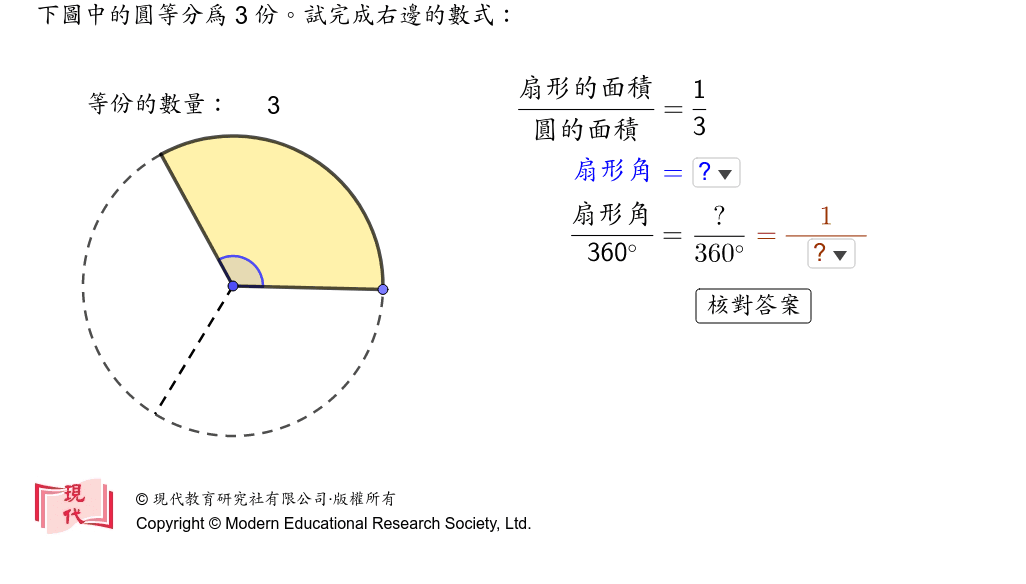
扇形面積公式 Geogebra

沪科版数学九年级下册24 7弧长与扇形面积 2 教案下载 Word模板 爱问共享资料

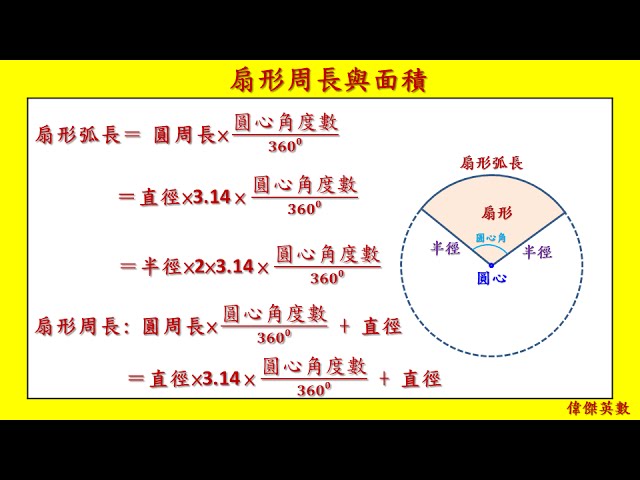
扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube

弧长公式扇形面积公式 西瓜视频搜索

Q Tbn And9gcqpqxxknzceay3mjcxzcklaz Iozcfat84mkqdgzflcwlamy23 Usqp Cau

弧长及面积公式 腾讯视频

弧长及面积公式 腾讯视频

圆中有关计算 弧长 扇形面积和圆锥

弧长和扇形面积 圆ppt课件3 Ppt课件下载 人人ppt

Q Tbn And9gcr6gw9fhpzovmfob2ngp9u Gvimmrq94zqc64t Ysfbxqs9wsbi Usqp Cau

圓的周長與面積 15 如何計算扇形的弧長 Youtube

九年级数学上册24 3圆与多边形4弧长扇形面积圆锥表面积计算课件 新人教版 莲山课件

1x秋九年级数学上册第二十四章圆24 4弧长及扇形的面积第1课时弧长和扇形面积教案2 新版 新人教版下载 Word模板 爱问共享资料

已知扇形aob的周长是6cm 其圆心角是1弧度 该扇形的面积为

扇形面积公式讲解 北京爱智康

扇形的面积 弧长 周长 弦长在线计算器 三贝计算网 23bei Com

圓的周長與面積 16 扇形弧長計算的練習 Youtube

扇形面积的计算公式的应用 28 5弧长和扇形面积的计算 初中冀教版13版 数学中国网 Mathschina Com

扇形面积公式 弧长和扇形面积 52fmz购物网

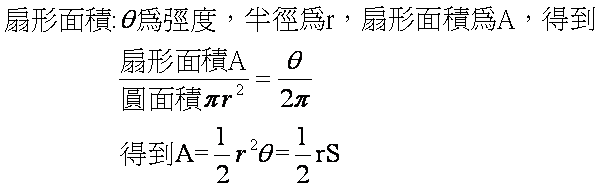
扇形的弧長與面積

圆扇形与弓形

扇形面积计算公式如何推导 教育频道 手机搜狐

人教版九年级上数学 24 4弧长和扇形面积 练习题 含答案 七七文库www 77wenku Com

弧长及扇形的面积公式 弧长及扇形面积计算公式

扇形弧长公式 扇形弧长公式画法

数 你好看 任意角三角函数与诱导公式 知乎

扇形的弧長與面積

弧长和扇形面积 圆ppt 第一课时 第一ppt

扇形的弧長公式 Youtube

弧长公式扇形面积公式 搜狗图片搜索

圆的周长与面积 弧长 扇形的面积 玄数

扇形面积公式和弧长公式 腾讯视频

扇形面积公式和扇形弧长公式扇形的所有公式

扇形周长公式和面积公式是什么 星火网校

高一 高一期末复习专题 6 弧长公式 扇形面积公式

扇形面积和弧长公式 搜狗搜索

弧长和扇形面积 圆ppt下载 第一ppt

九年级数学 圆 弧长和扇形面积 3u文域

高中數學 三角函數 數乙 弧長與扇形面積公式i 曾政清 Youtube

弧长公式 腾讯视频

证明扇形面积与弧长公式圆锥的侧面积为什么会等于prl 扇形面积公式推导兀rl 桃丽网

中考数学圆中弧长及扇形的面积计算专题 1 每日头条

弧长公式扇形面积公式 西瓜视频搜索

扇形弧长公式 扇形弧长公式画法

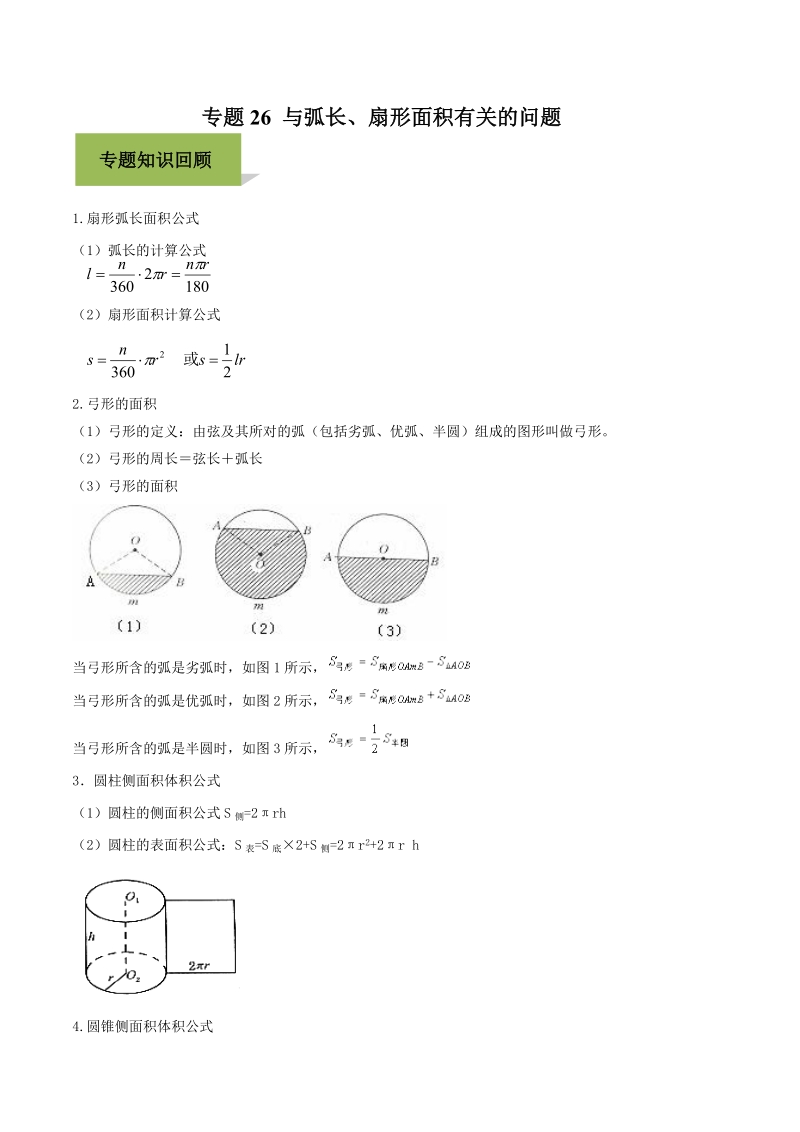
年中考数学必考专题26与弧长 扇形面积有关的问题 解析版 七七文库www 77wenku Com

九年级数学上册24 4弧长及扇形的面积24 4 1弧长和扇形面积 学案 新人教版 Doc 课件巴巴kejian Com 课件巴巴kejian Com

九年级数学 圆 弧长和扇形面积 3u文域

3 9 弧长及扇形的面积 哔哩哔哩 Bilibili

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

弧长的公式 扇形面积公式及其应用

扇形弧长及面积 每日头条

Ch2三角函數 2 1 2 2 我的m讚

扇形的周长和面积公式是什么 酷知经验网

圆中有关计算 弧长 扇形面积和圆锥

第24章弧长与扇形面积一扇形的弧长为10cm它的面积为24平方厘米 则此扇形的半径为

弧长和扇形面积下载 Word模板 爱问共享资料

扇形弧長及面積 每日頭條

功課幫

扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili

圆中有关计算 弧长 扇形面积和圆锥

弧长的公式 早旭阅读网

数 你好看 任意角三角函数与诱导公式 知乎

扇形弧長 扇形弧長是扇形的兩條半徑之間的圓弧長度 一條圓弧和經過這條圓弧 百科知識中文網

弧长和扇形面积公式 搜狗图片搜索

扇形周长 弧长公式和扇形面积公式 52fmz购物网

题型 2弧长与扇形面积公式的计算 哔哩哔哩 つロ干杯 Bilibili

三角公式怎么记 请看这儿

弧长公式扇形面积公式 西瓜视频搜索

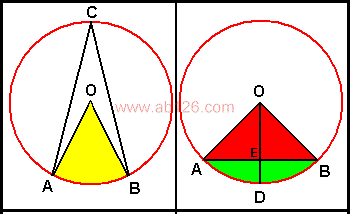
扇形弧长与面积公式在线计算器 在线计算 在线计算器 计算器在线计算